Ion probe (or SIMS) geochronology has no shortage of acronyms. SHRIMP is the most obvious one, and that in turn has spawned a number of associated abbreviations, such as PRAWN, ZOC, and the various standards (QGNG, FC1, SL13 BR266, etc.). In SHRIMP (and other SIMS- CAMECA stands for something in French) analysis, standards are used because the ionization efficiency of both Pb and U is variable, so you need something with a known Pb/U ratio to correct for these effects. One of the current popular standards is called TEMORA.
So I shouldn’t have been surprised when an American visitor to the RSES at the ANU asked me what TEMORA stood for. I wish I had a snappy answer. Perhaps he was expecting something like
Thermally Equilibrated Magnetite-Orthoclase Rhyolitic Assemblage*
Or
Time Evidently Made One Resplendent Anchorpoint
Or
The Excellent Mother Of Radiogenic Architypes
Because the boring truth is that it doesn’t stand for anything. Temora is the name of a town in Western NSW. The standard comes from a specific outcrop of the Middledale gabbroic diorite, and the particular outcrop from which this zircon was extracted happens to be on the road to Temora. Like most sources of zircon standards, this is an evolved mantle melt.
Crustal rocks are generally not chosen for zircon standards, as the zircons in crustally derived igneous rocks have a greater chance of being inherited from the source rock. This would make them older than the igneous zircons, giving your ‘standard’ two populations with different ages. This particular gabbroic norite from the fields near Temora was found to be fairly well behaved, isotopically speaking, so it has been widely used as a U/Pb, Hf isotope, and oxygen isotopic standard.
As for the town of Temora, it is a small country town in winter wheat and sheep country. It’s main claim to fame is the aviation museum, which keeps a number of vintage aircraft in flying condition and occasionally puts on shows.
The Temora zircon was called TEMORA 1 in the paper that originally described it. I have no idea why it was capitalized in this way. But it’s not an acronym. Perhaps the author just needed to yell to be heard from that far out in the bush.
* This would be wrong: It’s a gabbroic diorite.
I'm a geochemist. My main interest is in-situ mass spectrometry, but I have a soft spot in my heart for thermodynamics, poetry, drillers, trees, bicycles, and cosmochemistry.
Saturday, February 26, 2011
Thursday, February 17, 2011
Rare Earth Revelry four: Yttrium aluminum garnet
OK, so this is not really geology. YAG is not a naturally occurring mineral, and yttrium is only a REE wannabe. But REE-doped YAG is used in a variety of technological applications that enable geochemical analyses, such as Nd-YAG lasers that form the core of the low-end laser ICPMS systems.
I’m posting because I have heard of YAG for years and years, but never figured out what YAG actually was until tonight, when I got sidetracked in wikipedia.
Garnet is a mineral structure. It is a complex cubic structure that has a formula X3Y2Z3O12. The X site has a distorted 8-fold coordination, the Y site has 6-fold octahedral coordination, and the Z site has tetrahedral coordination. This tetrahedral site is trpically occupied by silica tetrahedrons in the case of most natural garnets, such as almandine, the typical crustal garnet: Fe3Al2(SiO4)3

The most common coupled substitution is the formation of majorite garnet at high pressure. Pyrope is magnesium aluminum garnet: Mg3Al2(SiO4)3. At high pressure, however, Si can start substituting into the octahedral coordination. Despite this pressure increase, magnesium can also still squeeze into the octahedral site, so the substitution is Mg+Si -> Al2. The resulting mineral, Mg3MgSi(SiO4)3, has a formula unit that simplifies to Mg4Si4O12, or MgSiO3. This is the same formula unit as enstatite (magnesium orthopyroxene), and indeed the transition of enstatite to majorite is one of the main transition zone reactions that marks the change from upper mantle to lower mantle mineralogy.
Yttrium aluminum garnet also has a coupled substitution. Starting with almandine (Fe3Al2(SiO4)3, the Fe is replaced with Y, and the charge balance is maintained by replacing the Si with tetrahedrally coordinated Al. This gives a formula of Y3Al2(AlO4)3, or Y3Al5O12. Substitution of various REE (most commonly Nd) for Y then gives the mineral its unique optical properties via mechanisms which I do not understand.
Rare Earth Revelry
Week -1
Introduction
Week 1
Week 2
Week 3
Week 4
I’m posting because I have heard of YAG for years and years, but never figured out what YAG actually was until tonight, when I got sidetracked in wikipedia.
Garnet is a mineral structure. It is a complex cubic structure that has a formula X3Y2Z3O12. The X site has a distorted 8-fold coordination, the Y site has 6-fold octahedral coordination, and the Z site has tetrahedral coordination. This tetrahedral site is trpically occupied by silica tetrahedrons in the case of most natural garnets, such as almandine, the typical crustal garnet: Fe3Al2(SiO4)3

Figure 1: The garnet crystal structure.
Most natural garnet compositions consist of solid solutions between common +2 8-fold and +3 octahedral ions: Mg, Mn, or Ca substituting for Fe, and Fe3+ or Cr substituting for Al. However, coupled substitutions allow for more complicated compositional changes.The most common coupled substitution is the formation of majorite garnet at high pressure. Pyrope is magnesium aluminum garnet: Mg3Al2(SiO4)3. At high pressure, however, Si can start substituting into the octahedral coordination. Despite this pressure increase, magnesium can also still squeeze into the octahedral site, so the substitution is Mg+Si -> Al2. The resulting mineral, Mg3MgSi(SiO4)3, has a formula unit that simplifies to Mg4Si4O12, or MgSiO3. This is the same formula unit as enstatite (magnesium orthopyroxene), and indeed the transition of enstatite to majorite is one of the main transition zone reactions that marks the change from upper mantle to lower mantle mineralogy.
Yttrium aluminum garnet also has a coupled substitution. Starting with almandine (Fe3Al2(SiO4)3, the Fe is replaced with Y, and the charge balance is maintained by replacing the Si with tetrahedrally coordinated Al. This gives a formula of Y3Al2(AlO4)3, or Y3Al5O12. Substitution of various REE (most commonly Nd) for Y then gives the mineral its unique optical properties via mechanisms which I do not understand.
Rare Earth Revelry
Week -1
Introduction
Week 1
Week 2
Week 3
Week 4
Tuesday, February 15, 2011
Renewable energy and the price of coal
One of the key issues relating to climate change, energy independence, and pollution control is that coal-powered electricity is cheap, compared to the less environmentally destructive alternatives. As a result, one of the big goals (or dreams, depending on one’s point of view) is to make renewable energy as cheap as coal. However, there is an implicit assumption here that is often overlooked. That is that coal power is, and will always be, cheap. Since the price of coal is a significant portion of the cost of coal-based electricity, this assumes that coal prices will be low and constant. How does this assumption compare to the data?


Figure 1. The spot price for Australian thermal coal exports, last 5 years. (source)
As the above figure shows, the price of coal has varied by more than a factor of four over the past five years. Of course, most coal is sold on long term (and not always public) contracts which contain less volatility than the spot price, but the point is that like all resources, it is not (to borrow a phrase from a competing energy type) too cheap to meter. Even in the US, which is somewhat limited to exposure on world markets by its meager export facilities, the assumption that coal will always stay cheap is worth questioning. The USA may be facing a generation glut at the moment due to industrial scalebacks caused by the recession, but axing plans to diversify the energy base due to low current prices is not a good long-term policy.Saturday, February 12, 2011
2010 Arctic Sea Ice minimum winner
Due to extensive travel in the September/October time period, I forgot to post the winner of the 2010 Arctic sea ice minimum competition.

The winner was Atwasi, whose guess of 4851 +/- 82 slightly edged out James Annan at 4750 +/- 80. According to his comment, Atwasi is a geophysicist like last year’s winner, Hypocentre. James was the runner up for the second year in a row.
Atwasi may now nominate a blog subject of his or her choosing for me to flail at.
Is there any interest in guessing at the winter maximum this year?

Figure 1. Final results for the 2010 sea ice minimum.
The winner was Atwasi, whose guess of 4851 +/- 82 slightly edged out James Annan at 4750 +/- 80. According to his comment, Atwasi is a geophysicist like last year’s winner, Hypocentre. James was the runner up for the second year in a row.
Atwasi may now nominate a blog subject of his or her choosing for me to flail at.
Is there any interest in guessing at the winter maximum this year?
Thursday, February 10, 2011
Further consideration of the Kepler planets
A few days ago, I posted that a brief analysis of the size distribution of the Kepler planets suggests that the size distribution of planets in our solar system is unusual.
This hypothesis requires the lack of Earth-sized planets (compared to planets twice as large) to be real, and not a result of poorer detection efficiency for Earth-sized planets relative to slightly larger ones.
Commenter number one suggested that my figure two was not a convincing demonstration of this, and a comparison of planet size vs. spectral type (a proxy for effective temperature) or stellar radius would be more convincing. So here are those plots.
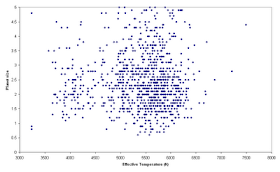

Figure 1 shows that earth-sized detections decrease for stars hotter than about 6000K, and figure 2 shows that they decrease for stars with a radius of more than 1.2 solar radii. This is not surprising, as the hotter stars will generally have larger radii, so a planet of a given size will block proportionally less light.
To correct for this, I have replotted a subset of the data release. Figure 3 is a probability distribution curve consists of only stars which have radii less than 1.1 times that of the Sun.

Filtering out the large radii stars leaves a sample size of 953. The general shape of the curve is not too different than the whole sample. So the hypothesis that the most common size of a planet is midway between Earth and Neptune still seems to hold.
This hypothesis requires the lack of Earth-sized planets (compared to planets twice as large) to be real, and not a result of poorer detection efficiency for Earth-sized planets relative to slightly larger ones.
Commenter number one suggested that my figure two was not a convincing demonstration of this, and a comparison of planet size vs. spectral type (a proxy for effective temperature) or stellar radius would be more convincing. So here are those plots.

Figure 1. Planetary radius (relative to Earth) vs. effective temperature.

Figure 2. Planetary radius (relative to Earth) vs. stellar radius (relative to the Sun).
Figure 1 shows that earth-sized detections decrease for stars hotter than about 6000K, and figure 2 shows that they decrease for stars with a radius of more than 1.2 solar radii. This is not surprising, as the hotter stars will generally have larger radii, so a planet of a given size will block proportionally less light.
To correct for this, I have replotted a subset of the data release. Figure 3 is a probability distribution curve consists of only stars which have radii less than 1.1 times that of the Sun.

Figure 3. Probability distribution curve of planets around stars with stellar radii less than 1.1 times that of the sun.
Filtering out the large radii stars leaves a sample size of 953. The general shape of the curve is not too different than the whole sample. So the hypothesis that the most common size of a planet is midway between Earth and Neptune still seems to hold.
Tuesday, February 08, 2011
Our planets are weird
The Kepler data release has delivered a huge amount of data on planets orbiting stars in our galaxy.
This survey is designed to detect planets as small as earth (or a little bit smaller), and the way it works means that it most easily detects planets that are very close to their host stars. So most of the stars in this survey orbit their host star closer than Mercury orbits the sun. Despite this, figure 1 shows that there is something very unusual about our solar system.

The most common planets in the Kepler survey have a radius of about twice that of the Earth, or about half that of Neptune. There are no such planets in our solar system. In fact, this gap is what we traditionally call the dividing line between ‘terrestrial’, or rocky planets, and giant planets (the giants are then further divided into the ice giants (Neptune and Uranus), and the gas giants (Jupiter and Saturn). There is nothing in between the ice giants and the rocky planets in this solar system. And yet, that is the most common size of planet in the Kepler survey.
There are a few caveats here. Firstly, is the peak is real or is an artifact related to the difficulty in finding earth-sized planets around dim stars? We can plot the magnitude of the star vs the size of the planet to determine this (figure 2).

If the Kepler abundance peak around 12600 km (2 earth radii) in figure 1 is related to difficulty in finding smaller planets around dimmer stars, then we would expect the high magnitude stars to show fewer planets with a radius between 1 and 2 earth radii (the lower right portion of the graph). This area does not appear to be under-populated. So that caveat appears to be irrelevant to this study.
Another caveat is that the planets seen so far are all close to their host stars, and may represent migrated outer planets. So the distributions may be biased by a process that did not occur in our solar system. We can look at the period vs size distribution to test this (figure 3). If the earth-sized and smaller planets are all similar to the planets in our solar system, then they may have similar orbits. If the larger planets are all scattered in from the outer solar system, then they may have a different orbital distribution.

What we see is that Kepler has not yet detected any earth-sized planets in periods as long as Mercury (much less Venus or Earth). That’s OK, such a detection is not expected for a few more years. All of the earth-diameter planets are in very short orbits. However, a few of the planets with a size intermediate between earth (1 earth radii) and Neptune (4 earth radii) have orbits that are broadly similar to that of Mercury or Venus. So these planets can not be definitively identified as scattered from their orbital period alone.
So, from the data we have so far, it appears that the galaxy is full of unfamiliar planets. Or, from the galaxy’s point of view, our solar system is devoid of normal planets, and only harbors oddballs.
Update:
See part 2 for further discussion of selection effects.
This survey is designed to detect planets as small as earth (or a little bit smaller), and the way it works means that it most easily detects planets that are very close to their host stars. So most of the stars in this survey orbit their host star closer than Mercury orbits the sun. Despite this, figure 1 shows that there is something very unusual about our solar system.

Figure 1. Green lines are the radii of the planets in our solar system. Earth and Venus are blended together at this scale. The red line is the probability distribution of planets in the Kepler survey.
The most common planets in the Kepler survey have a radius of about twice that of the Earth, or about half that of Neptune. There are no such planets in our solar system. In fact, this gap is what we traditionally call the dividing line between ‘terrestrial’, or rocky planets, and giant planets (the giants are then further divided into the ice giants (Neptune and Uranus), and the gas giants (Jupiter and Saturn). There is nothing in between the ice giants and the rocky planets in this solar system. And yet, that is the most common size of planet in the Kepler survey.
There are a few caveats here. Firstly, is the peak is real or is an artifact related to the difficulty in finding earth-sized planets around dim stars? We can plot the magnitude of the star vs the size of the planet to determine this (figure 2).

Figure 2. Magnitude vs. planetary radii Higher magnitude stars are dimmer.
If the Kepler abundance peak around 12600 km (2 earth radii) in figure 1 is related to difficulty in finding smaller planets around dimmer stars, then we would expect the high magnitude stars to show fewer planets with a radius between 1 and 2 earth radii (the lower right portion of the graph). This area does not appear to be under-populated. So that caveat appears to be irrelevant to this study.
Another caveat is that the planets seen so far are all close to their host stars, and may represent migrated outer planets. So the distributions may be biased by a process that did not occur in our solar system. We can look at the period vs size distribution to test this (figure 3). If the earth-sized and smaller planets are all similar to the planets in our solar system, then they may have similar orbits. If the larger planets are all scattered in from the outer solar system, then they may have a different orbital distribution.

Figure 3. Kepler planets plotted by period vs. radius. Colored dots are Kepler planets, white stars are Mercury, Venus, and Earth. Period is in days, radius is in earth radii (6372 km).
What we see is that Kepler has not yet detected any earth-sized planets in periods as long as Mercury (much less Venus or Earth). That’s OK, such a detection is not expected for a few more years. All of the earth-diameter planets are in very short orbits. However, a few of the planets with a size intermediate between earth (1 earth radii) and Neptune (4 earth radii) have orbits that are broadly similar to that of Mercury or Venus. So these planets can not be definitively identified as scattered from their orbital period alone.
So, from the data we have so far, it appears that the galaxy is full of unfamiliar planets. Or, from the galaxy’s point of view, our solar system is devoid of normal planets, and only harbors oddballs.
Update:
See part 2 for further discussion of selection effects.
Sunday, February 06, 2011
Blogging on geologic timescales
Sorry about the quiescence. To make a long story short, work and family has been keeping me busy, and if that wasn’t enough, I have been trying to tidy up a manuscript I rough drafted over Christmas break.
Of course, this happens to everyone who keeps blogging after grad school, but in addition, the December-January period saw a large number of inquiries about instrumentation at work. Without going into details, this consists of questions from scientists around the world, who want to know something about how ion probes work. Inevitably, these questions result in me digging through a bunch of papers, synthesizing the results, and writing a brief, accessible explanation to their query. And with about 2500 SHRIMP papers and 750 from our competitor’s instruments, reading and memorizing everything isn’t an option. This rapid-turnaround science explanation process should sound familiar to anyone else out there who writes science blogs. The point being, that my explain-technical-science-on-short-notice fix has been coming from the office. Or the manuscript. So motivation has been low.
But, the manuscript is in, and work might be getting back to normal, so hopefully I’ll have a bit more to say in the near future.
In the mean time, I recommend reading the systemic blog for first impressions on the Kepler data release.
Of course, this happens to everyone who keeps blogging after grad school, but in addition, the December-January period saw a large number of inquiries about instrumentation at work. Without going into details, this consists of questions from scientists around the world, who want to know something about how ion probes work. Inevitably, these questions result in me digging through a bunch of papers, synthesizing the results, and writing a brief, accessible explanation to their query. And with about 2500 SHRIMP papers and 750 from our competitor’s instruments, reading and memorizing everything isn’t an option. This rapid-turnaround science explanation process should sound familiar to anyone else out there who writes science blogs. The point being, that my explain-technical-science-on-short-notice fix has been coming from the office. Or the manuscript. So motivation has been low.
But, the manuscript is in, and work might be getting back to normal, so hopefully I’ll have a bit more to say in the near future.
In the mean time, I recommend reading the systemic blog for first impressions on the Kepler data release.